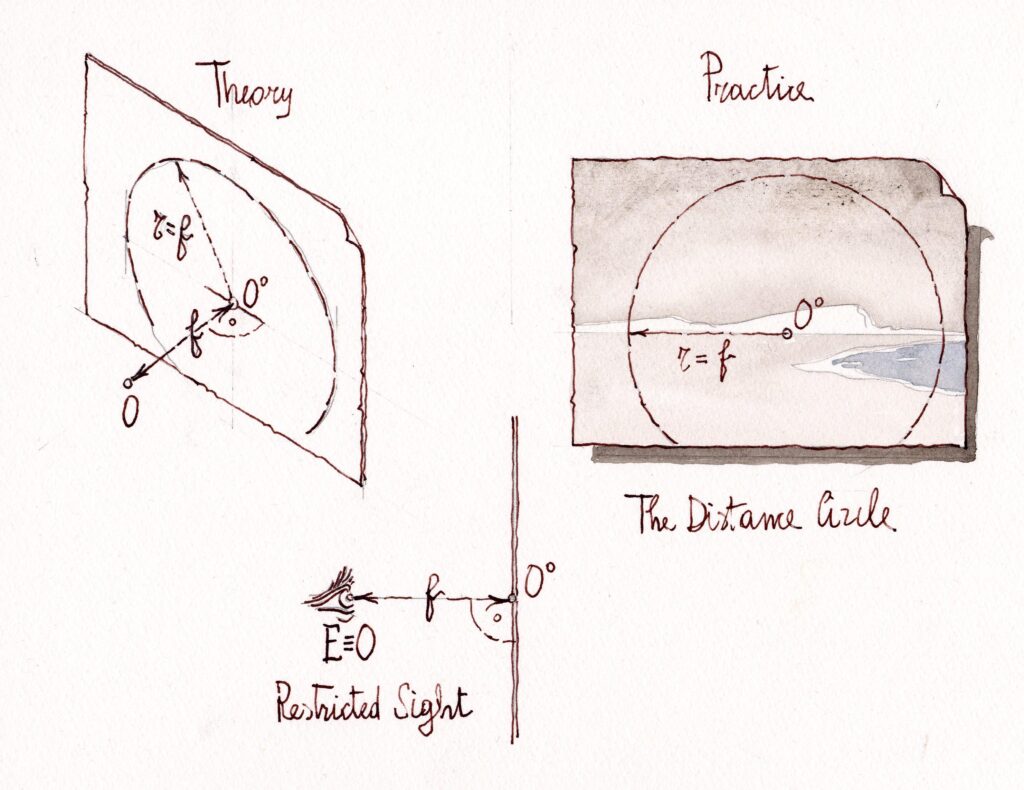
We draw a circle called distance circle. The centre of this circle is point O0, which is called Principal Point. The radius
of the distance circle is equal to the distance from the eye (projection centre) to the picture plane and the projection
centre belongs to the perpendicular straight line passing through O0.
Measure the distance from the projection centre to the picture plane: this distance ‘f’ is the Principal Distance of the perspective, equivalent to the focal length in photography. Therefore f = (OO0).
The distance circle, having the radius equal to the principal distance, represents the projection centre and allows to place this in the space relative to the picture plane. For this purpose we use the following convention.
The centre of projection is located on the perpendicular that is conducted to the principal point at a distance to the picture plane equal to the radius of the distance circle.
In practice.
Draw a circle whose diameter is close to the width of the paper. The projection centre O will be on the perpendicular to the paper passing through the principal point O0 (centre of the distance circle).
Notes
To obtain the restricted sight, the eye must be placed in point O, in the space that is in front of the paper. In the above-said position, the eye can rotate freely.